Equinor CTF 2024

Equinor CTF is an annual onsite CTF in Norway. I played with my team Norske Nøkkelsnikere, and we placed 5th out of 79 teams and during the CTF I got two first bloods!

crypto

👶 Double Dip Dilemma 👶 🩸

Autor: starsiv

Description: We intercepted some encrypted communication we think is very important. But it appears they are using untraceable OTP. We have two ciphertexts from the communication, and also the plaintext for the first. Can you help decrypt the second?

We are given a intercept.txt file that contains two plaintexts and two ciphertexts. The ciphertexts are encrypted with a One-Time Pad (OTP), which is a very simple form of encryption that relies on bitwise XORing a message with a random binary sequence. Since the OTP is deterministic, we can use the inherent properties of XOR to recover the key.

Vulnerability

OTP key reuse

The one-time pad is theoretically unbreakable when used correctly. However, its security relies on two critical factors:

The key must be truly random
The key must never be reused

In this challenge, the second rule is violated, since we are given two plaintexts and two ciphertexts that are encrypted with the same OTP key. By reusing the OTP key, the system becomes vulnerable to a known-plaintext attack.

The attack

The attack exploits the properties of the XOR operation used in OTP encryption:

Let's denote:

$P_1$ and $P_2$ as the two plaintexts
$C_1$ and $C_2$ as the two ciphertexts
$K$ as the OTP key

In OTP encryption, the ciphertext is produced by XORing the plaintext with the key: $C = P \oplus K$

Since we know $P_1$ and $C_1$ , we can recover the key: $P_1 \oplus K = C_1$ , then $K = P_1 \oplus C_1$

Once we have $K$ , we can decrypt any message encrypted with this key: $P_2 = C_2 \oplus K$

By substituting our recovered key: $P_2 = C_2 \oplus (P_1 \oplus C_1) = C_2 \oplus P_1 \oplus C_1$

Solution

For first solving the challenge, I used CyberChef since it was the fastest way to get the solution, when I recognized the OTP vulnerability. This lead me to a first blood on this introductory crypto challenge.

For a more technical and in-depth writeup, please check out Sithis from bootplug's writeup. In the end I wrote a simple solve.py script that will print out the whole message:

Limit your messages to 100chars to fit the master OTP. Now use this secret: EPT{w3lc0m3_t0_my_kr1b!}

The flag is: EPT{w3lc0m3_t0_my_kr1b!}

LFSXOR

Autor: Surprior

Description: We are given a out.bmp file and a enc.py script. Upon first glance, we can see that the image is encrypted and contains a lot of noise.

Code analysis

import sys

import numpy
import matplotlib.pyplot as plt
from PIL import Image


def get_rand(x):
	def _random():
		nonlocal x
		x ^= (x << 14) & 0xFFFFFFFF
		x ^= (x >> 6) & 0xFFFFFFFF
		x ^= (x << 11) & 0xFFFFFFFF
		return x & 0xFF
	return _random


def encrypt(in_img, out_img, key):
	in_img = plt.imread(in_img)[:, :, 0]
	height = len(in_img)
	width = len(in_img[0])
	
	imarr = numpy.zeros((height, width, 3), dtype='uint8')
	rand = get_rand(key)
	
	for y in range(height):
		for x in range(width):
			imarr[y,x] = int(in_img[y,x] ^ rand())
	
	im = Image.fromarray(imarr.astype('uint8')).convert('RGB')
	im.save(out_img)


if __name__=='__main__':
	IN_IMG = sys.argv[1]
	OUT_IMG = sys.argv[2]
	KEY = int(sys.argv[3])
	encrypt(IN_IMG, OUT_IMG, KEY)

We are presented with a program that encrypts an image using an LFSR for generating PRNG out of a key and XOR that with a pixel from the original image. Something that I noticed straigh away was that if we dismiss the LFSR functionality in the get_rand function that implements the LFSR, and just look at the return value, it will only return a value between 0-255 no matter what the value of x is (in our case the key).

We can see this with the following code:

def get_rand(x):
  def _random():
    nonlocal x
    x ^= (x << 14) & 0xFFFFFFFF
    x ^= (x >> 6) & 0xFFFFFFFF
    x ^= (x << 11) & 0xFFFFFFFF
@>  return x & 0xFF
  return _random

Since the bitwise AND operation with 0xFF (binary 11111111) effectively masks the result to the least significant 8 bits. Since 8 bits can represent 256 distinct values as $2^8$ , the function will only return integers from 0 to 255 inclusive, no matter what the value of x is. In our case it was the original key.

This means, we could just directly XOR the encrypted image with values from 0-255 and analyze the noise and hope we see something of interest. We do not aim for a clear image, only a good enough picture where we hopefully can see something.

Solving the challenge

Knowing that the image containing the flag is encrypted by XORing a key with values between 0-255, I wrote a Python script to decrypt the image with every possible key, save the results, and print the time taken for the process, allowing me to work on another challenge while waiting for the script to finish.

import sys
import numpy
import matplotlib.pyplot as plt
from PIL import Image
from enc import get_rand
import time

def decrypt(in_img, key):
    in_img = plt.imread(in_img)[:, :, 0]
    height, width = in_img.shape
    
    imarr = numpy.zeros((height, width, 3), dtype='uint8')
    rand = get_rand(key)
    
    random_values = numpy.array([rand() for _ in range(height * width)], dtype='uint8').reshape(height, width)
    
    # xor but vectorized  efficiency and speed
    imarr[:, :, 0] = (in_img ^ random_values)  # just edit first channel
    imarr[:, :, 1] = imarr[:, :, 0]  # copy to other channels for RGB
    imarr[:, :, 2] = imarr[:, :, 0]
    return Image.fromarray(imarr.astype('uint8')).convert('RGB')

if len(sys.argv) != 2:
    print("Usage: python main.py <input_image>")
    sys.exit(1)

IN_IMG = sys.argv[1]

start_time = time.time()
for key in range(1, 256):
    decrypted_image = decrypt(IN_IMG, key)
    out_img = f"{key}.png"
    decrypted_image.save(out_img)
    print(f"Saved: {out_img}")
    
    if key % 5 == 0:
        elapsed_time = time.time() - start_time
        print(f"Time taken for {key} images: {elapsed_time:.2f} seconds")
        estimated_total_time = (elapsed_time / key) * 255
        print(f"Estimated total time for 255 images: {estimated_total_time:.2f} seconds")

Extracting the flag

After XOR-ing the image with all possible keys, I uploaded one of the decrypted images to AperiSolve. The image contained a lot of noise, and I just hoped to find something recognizable. Interestingly, the images revealed the flag when viewed in AperiSolve's superimposed noise view and color view.

Each image corresponds to a different key, resulting in varying levels of noise, hence I just inputted a random image and hoped for the best. This particular image was clear enough to discern the flag amidst the superimposed noise.

From this point, we read out the letters we could see and made an educated guess about the flag's content and submitted it.

Flag: EPT{DOUBLECRYPTOTOFAIL}

misc

Leftovers 🩸

Autor: starsiv

Description: Our "employee of the week" eloped. He was the only one that knew the master class secret. We managed to extract logs from his last activities. Can you find anything from this?

We are given a terminal log from a user, where the user is encrypting a file called master.txt with openssl. It uses the hostname as the password and the current time as the number of iterations, and the encryption algorithm is AES-256-CBC with PBKDF2 key derivation. At last it is encoded with base64.

Full command:

openssl enc -aes-256-cbc -pbkdf2 -iter $ITER -in master.txt -k $PWD -a

Output:

U2FsdGVkX1+/39qrCQ9rlxMW2E30ylTUXYS+GTAVDMUK0oXJvkUDBCRbhClK2GKYc50OQZ7zgLPBhkMW8CM5VVnZBrxfyH5CAG8nj5BPDCg=

Solution

AES-256-CBC is a symmetric encryption algorithm, which means that the same key and iterations are used for encryption and decryption.

Since we know the hostname and the iteration count from the terminal log, we can decrypt the file using the same command but with the decryption flag -d.

Save the output to a file called encrypted.txt and run the following command to decrypt it:

openssl enc -aes-256-cbc -pbkdf2 -iter $ITER -d -a -in encrypted.txt -k $PWD

The output is the flag.

Master class secret: EPT{Ach13v3m3nt_Unl0ck3d_293857}

Flag: EPT{Ach13v3m3nt_Unl0ck3d_293857}

Canvas Curve

Autor: mattis

Description: You know the drill, collect apples for points, profit and flags! Gather up to 4 team members to help collect apples.

To solve this challenge, we need to play the game snake until we collect 1000 apples. But who said we need to play the game?

Analysis

We can read the source code of the game with the browser's developer tools which exposes the game logic. We see that we have a pixel.js file that contains a lot of pixel data and a game.js file that contains the game logic, and upon inspecting this game.js file we can see that the random apple that we need to collect is initialized with the same seed for each run. Having the same seed means that the apples will end up in the same place every time when the game is finished.

this.randomAppl = new randomApple(1234);

With this knowledge, we see that the randomApple function is defined in the randomApple.js and is looking complex and hard to understand.

class randomApple {
  constructor(s) {
    this.modulus = 2 ** 31 - 1; 
    this.multiplier = 48271; 
    this.increment = 0;
    this.s = s % this.modulus;
    if (this.s < 0) this.s += this.modulus; 
  }

  n() {
    this.s = (this.multiplier * this.s + this.increment) % this.modulus;
    return this.s / this.modulus;
  }

  next(min, max) {
    return min + Math.floor(this.n() * (max - min + 1));
  }
}

Solution

Since we can download the game from the challenge page, and run it locally, we can modify the game logic to reveal the flag when we collect 1000 apples, since we know the seed and the output of the randomApple function would be deterministic.

I revealed this with editing the game.js file, and making it automatically collect the current apple and move to the next apple until we have collected 1000 apples, and the game will print the flag.

if(this.collectedApples.length < 1000) {
  // Automatically collect the current apple
  this.collectedApples.push(this.apples[this currentApplePosition]);
  delete this.apples[this.currentApplePosition];
  // Move to the next apple
  this.currentApplePosition = this.randomAppl.next(0, 409000);
  ...
}

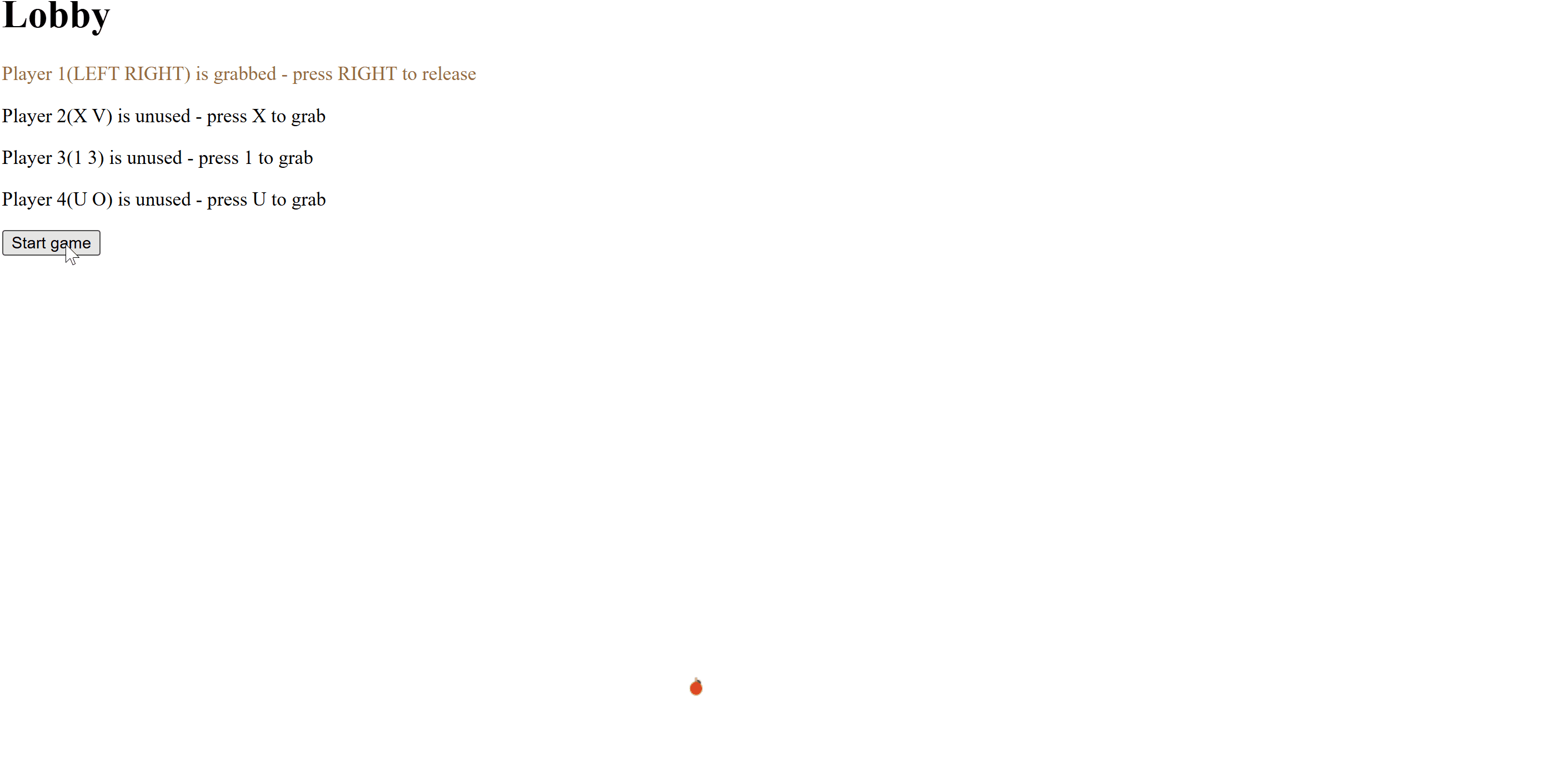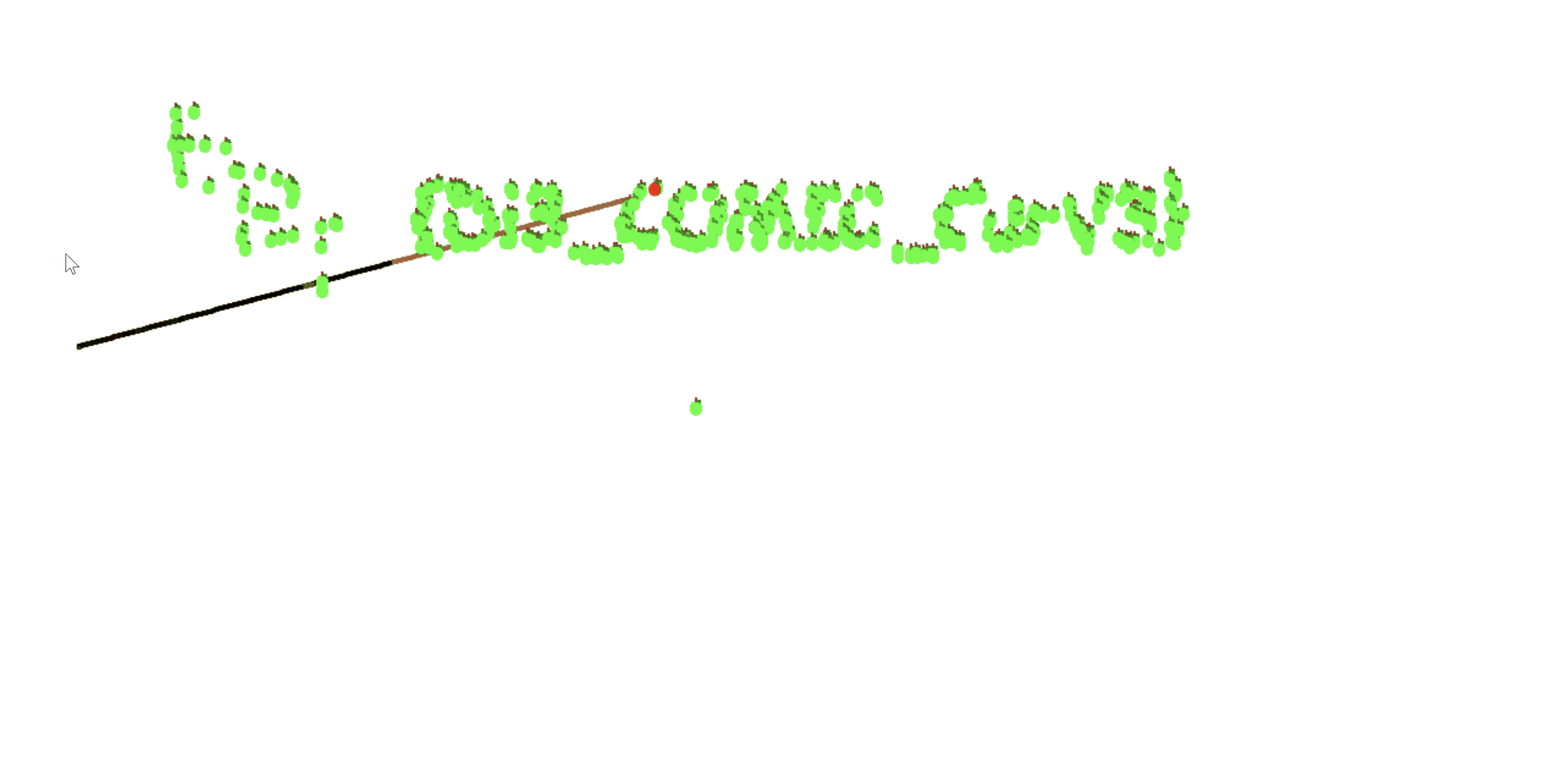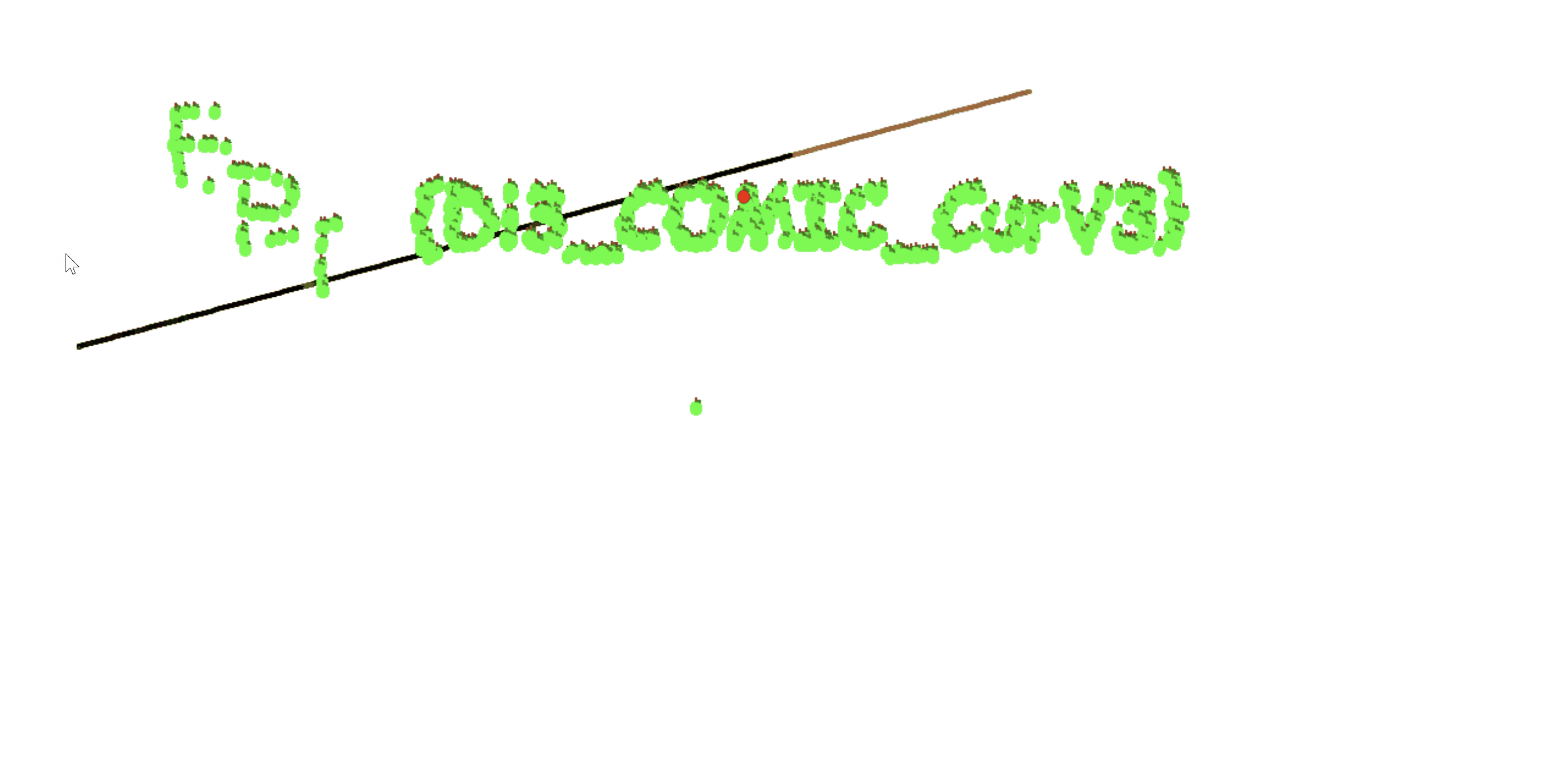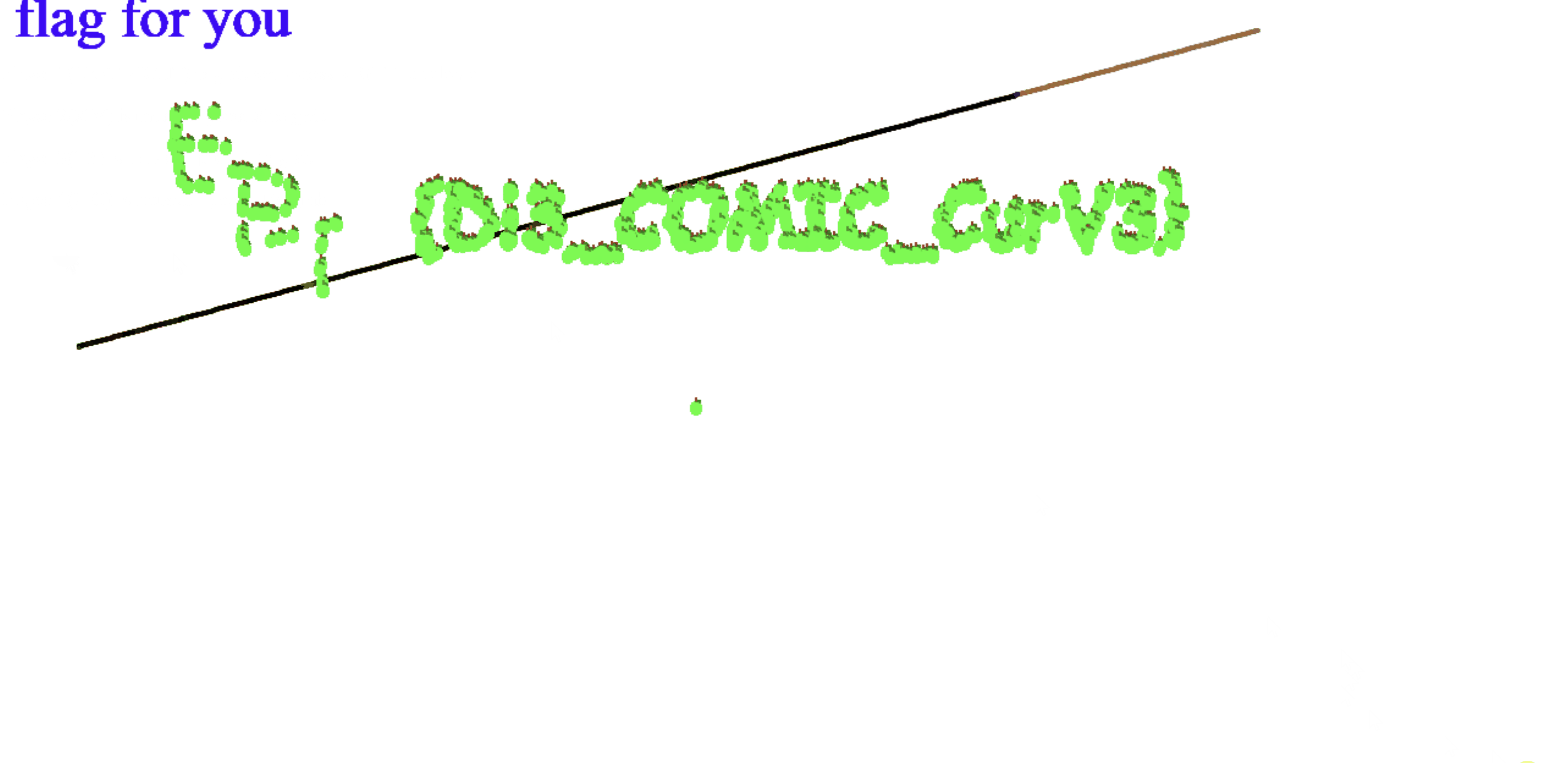
Flag: EPT{DI3_COMIC_CurV3}

🔥 Pixel Perfect 🔥 🥈

Autor: nordbo, tmolberg, null

Description: Something in your surroundings just changed. What?!

Decode the message displayed on a wall with 16 static lights and moving color pairs. The key is to interpret the color combinations as ASCII characters in hexadecimal. For making it easier, map out the section where the start of the flag is displayed, EPT{, and begin decoding from there.

While this, also account for the color ambiguities due to lighting conditions lol

Flag: EPT{c0l0r_m3_h4ppy}